Nonadiabatic dynamics
When a molecule absorbs a photon in the UV or visible range, the energy goes to its electrons, whose configuration is changed in comparison to the ground state electronic density. The probability of absorbing a photon as a function of its wavelength – the absorption spectrum – is discussed in the “UV/Vis spectrum simulations“. Here, we will be concerned with what happens after the absorption.
The new electronic density generated right after the photon absorption does not, in general, correspond to an equilibrium state of the molecule. This means that there are forces acting on the atoms, inducing conformational changes (adiabatic process).
Dynamics simulation in the excited states is a great method for monitoring how these changes take place. You can know more about the change itself in “Nonadiabatic ultrafast phenomena“.
There are a few main challenges concerning excited state dynamics:
-
First, the potential energy of the excited state is normally much more complicated than that of the ground state. This means that we cannot use simple potential energy models as in molecular mechanics to compute the forces. Their computation should be done by solving the Schrödinger equation, which means that we have to deal with very high computational costs.
-
The potential energy of the electronically excited state in which the molecule is excited is often very near the potential energy of other excited states. For this reason, the molecule can jump to these other states during the relaxation (nonadiabatic process). We have also to deal with such possibility.
-
The relaxation dynamics may proceed through several different pathways. These several ways should be mapped and their relative importance evaluated.
The main method that we use in our group to investigate excited-state dynamics is the surface hopping approach, which was proposed by Tully and Preston in the early 1970’s (see review in Ref). This is a semiclassical method which allows keeping the computation costs under control.
In surface hopping, the challenges enumerated above are addressing in the following way:
-
The adiabatic processes are treated by solving Newton’s equations for the nuclei under the excited-state forces.
-
The nonadiabatic processes are treated by simultaneously computing the transition probability to other states and stochastically evaluating whether the molecule should stay in the same state or jump to another one.
-
The multiple reaction pathways are evaluated statistically by following a large number of trajectories starting with different initial conditions.
All these procedures are performed with the Newton-X program package, which we have specially developed for computing surface hopping.
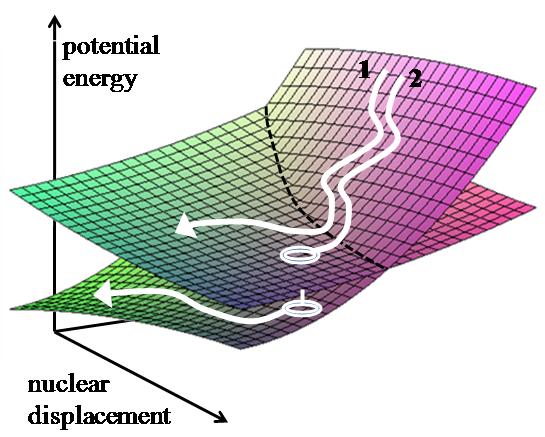
Two trajectories starting with the same initial conditions may have different fates due to the stochastic nature of the method.
Numerical nonadiabatic couplings
One of the main bottlenecks of nonadiabatic simulations is the computation of nonadiabatic couplings, which are the terms that connect different electronic states. These couplings are not usually available in standard quantum chemical programs for most of the quantum-chemical methods. An alternative to the explicit computation of the nonadiabatic couplings is to compute the time-derivative couplings as proposed by Hammes-Schiffer and Tully.
Time-derivative couplings can be evaluated numerically by computation of wavefunction overlaps along the trajectory. We have implemented this method in Newton-X to be used with MRCI, MCSCF (Ref), and TDDFT (Ref), CC2 and ADC(2) (Ref) approaches.
This same approach can be used for spin-orbit couplings as well.
Nonadiabatic dynamics with QM/MM
Nonadiabatic dynamics simulations can also profit from hybrid schemes such as QM/MM. The atoms of the entire system S to be treated by means of the hybrid method are divided into disjoint regions. For a standard QM/MM-setup with electrostatic embedding, these subsets are typically an inner and an outer region. Inner and outer region are described by quantum mechanics and molecular mechanics, respectively. Specifically, QM electronic-structure methods are used to accurately describe multiple electronic states of the compound of interest, while the MM component primarily deals with secondary environmental effects. Standard force fields are employed in the MM part incorporating bonded terms, van-der-Waals interactions and electrostatic interaction between partial point charges associated with each atom. Our implementation of QM/MM surface hopping is described in Ref.
Special care should be taken of the initial conditions for the dynamics. To take them from a Wigner distribution, as usually done for small molecules, is not practical. On the other hand, to take the initial conditions from a thermalized MM trajectory in the ground state tends to generate too cold initial ensemble for the QM region (Ref). We have devised a way to avoid these problems by combining Wigner distribution for the QM part and thermal configurations for the MM part. The exact procedure is explained in Ref.
An example of a single trajectory computed with surface hopping QM/MM dynamics is shown in the movie below for Me-formamide (Ref).