Spin-Orbit Couplings Based on Density Functional Theory

PySOC, a new program for fast and flexible computation of spin-orbit couplings.

We have developed a new versatile code based on Python scripts to calculate spin-orbit coupling (SOC) elements between singlet and triplet states, including both ground and excited states. The code, named PySOC, has been developed by Xing Gao, former postdoc at Walter Thiel‘s group, in collaboration with my group in Marseille and Thomas Niehaus in Lyon.

SOC plays a fundamental role in spin-forbidden excited-state processes, such as intersystem crossing and phosphorescence. From the computational chemistry standpoint, with the increasing popularization of dynamics simulations for studying excited states and charge transport, there is a vivid demand for new methods to efficiently evaluate SOC elements. PySOC targets this demand, with SOC computations using DFT-based methods

In this first version, PySOC is interfaced to Gaussian 09 and DFTB+ codes. SOCs are evaluated on the basis of time-dependent density functional theory (TDDFT), TDDFT with Tamm-Dancoff approximation (TDA), and time-dependent density functional tight binding (TD-DFTB); all three solved within linear-response approximation and using Casida’s wave functions.

In the past, two routes have been pursued to calculate SOCs in DFT-based methods: i) variational methods in the zeroth-order regular approximation (ZORA) Hamiltonian, and ii) perturbative methods. In PySOC, we followed the second route, adopting the Breit-Pauli (BP) spin-orbit Hamiltonian with effective charge approximation.

SOCs calculated with PySOC were benchmarked for several organic systems, spanning different orders of magnitude of SOC values.

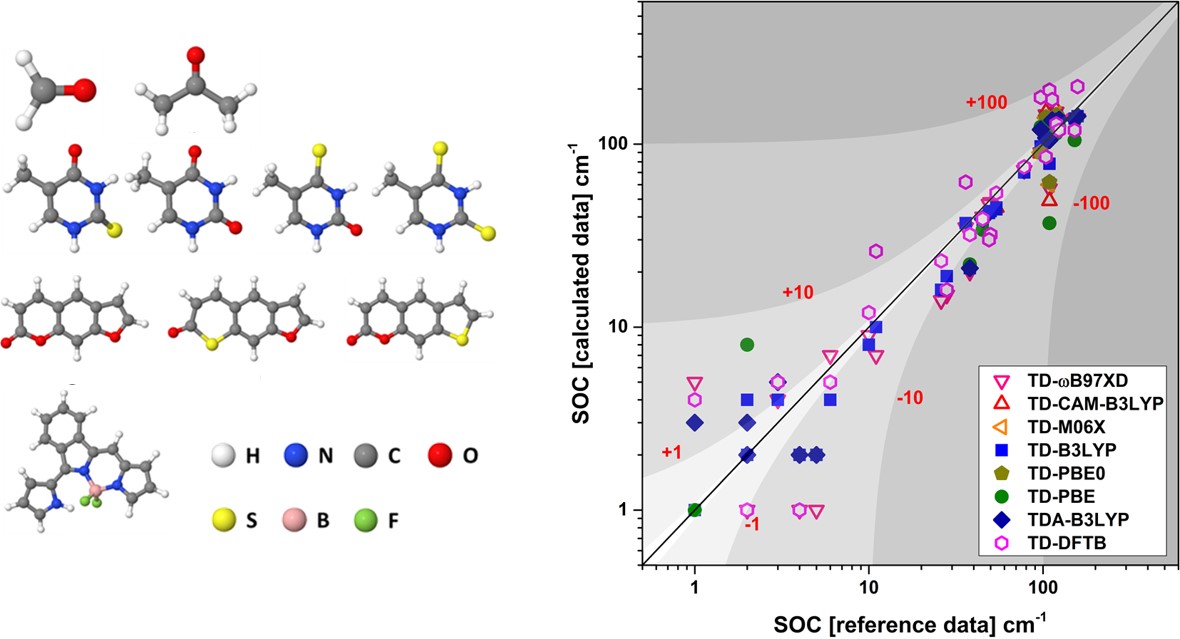
(Left) Molecules included in the benchmark. (Right) PySOC results with different methods against reference SOC values.

The computed SOCs show little dependence on the basis set, however, they are sensitive to the density functional considered. The benchmark results are in good agreement with reference data obtained using higher level spin-orbit and electronic Hamiltonians.

We found out that the methods currently implemented in PySOC predict SOC values for weak couplings (0-10 cm^-1) very well, with deviations of ca. 1 cm^-1. For strong couplings (100-200 cm^-1), the agreement with the reference data ranges from semi-quantitative (ca. 10 cm^-1 deviation) to qualitative (ca. 100 cm^-1 deviation), depending on method, density functional, and density functional parameterization.

Generally, the accuracy improves along the following orders:

1. Functionals: pure < hybrid ≈ range-separated
2. Methods: TD-DFTB < TDA < TDDFT

In the case of range-separated functionals, the predicted SOC values strongly depend on the range-separation parameter.

TD-DFTB, on its turn, although it shows the largest deviations, may still be useful for the treatment of very large molecular systems (hundreds of atoms), since it correctly predicts general trends at extremely low costs.

Calculations with PySOC are very fast. The initial linear-response calculation is typically the computational bottleneck of SOC evaluations, and the final cost is basically that of computing energies for the singlet and triplet states of interest.

PySOC and the SOC benchmark are discussed in a recent publication at the JCTC [1].

The program can be freely obtained by directly contacting Xing Gao.

Reference

[1] X. Gao, S. Bai, D. Fazzi, T. Niehaus, M. Barbatti, and W. Thiel, Evaluation of spin-orbit couplings with linear-response time-dependent density functional methods; doi:10.1021/acs.jctc.6b00915 (2017). doi:10.1021/acs.jctc.6b00915