Semiclassical simulations
UV/vis spectrum simulations using the nuclear-ensemble approximation (Ref) were recently implemented in the Newton-X program for simulations with the MRCI, CASSCF, TDDFT, CC2, ADC(2) and DFT/MRCI methods. These simulations can also be used for initial conditions generations for excited-state dynamics starting from multiple electronic states (Ref).
The spectrum is simulated by sampling the ground state nuclear geometries either by a statistical distribution (for instance, a Wigner distribution) or by a trajectory run. Then, for each of such geometries Rk, the excitation energies ΔE and the oscillator strengths f into the states of interest are computed
With these results, the absorption cross section can be computed, which is related to the extinction coefficient by
The spectra computed in this way can be directly compared to experiments in absolute units. Simulation costs about 500 single point calculations (no gradients needed). In general, a good qualitative agreement is observed, although no vibrational progression can be simulated.
The usage of the method for computation of photoionization cross sections is discussed in Ref.
More recently, we have shown how importance sampling techniques can be used with the nuclear ensemble approach to recompute spectra without re-doing the quantum chemical calculations.
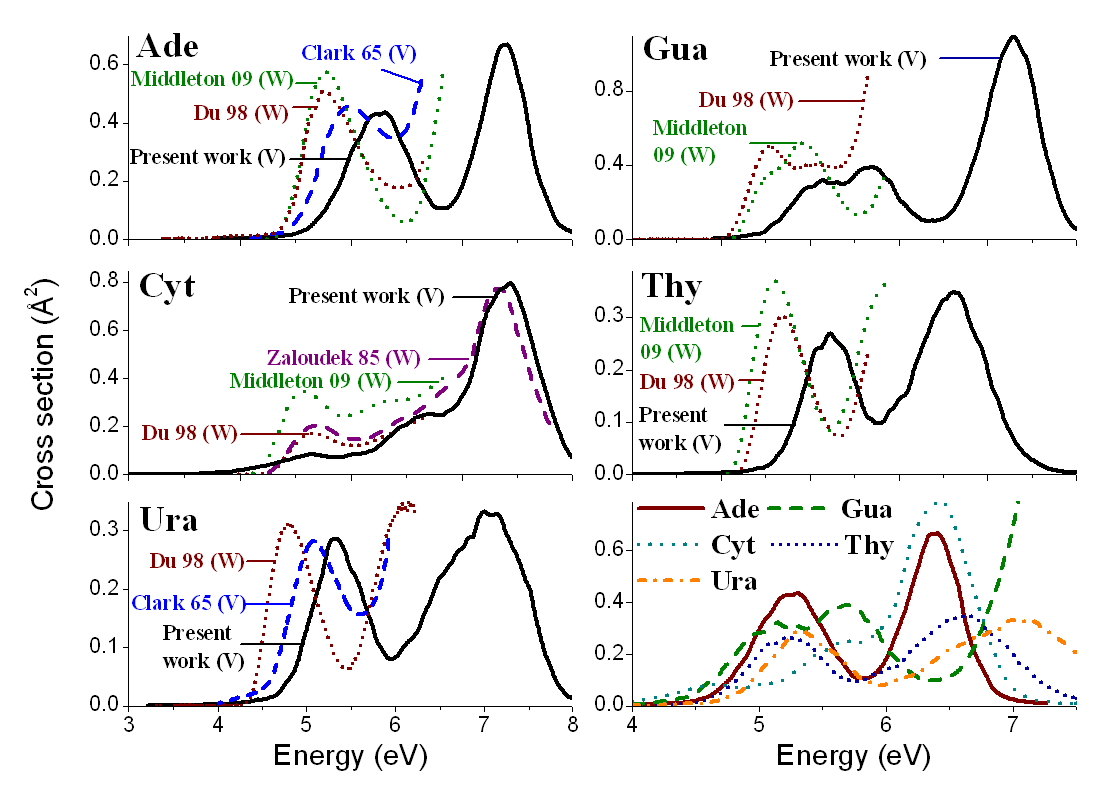
UV spectra of nucleobases (Ref).
Vibronic couplings
The semi-classical approach is a post-Condon approximation. Therefore, vibronic couplings are naturally included. We have shown in Ref that weak vibronically coupled peak of azomethane can be obtained with a quality similar to that obtained with full quantum mechanical methods (if vibrational progressions are neglected). Spectrum simulations with symmetry restrictions were computed in Ref for Cr(CO)6, allowing the assignment of several vibronic coupling features.
Tautomeric effects
When multiple tautomers are present, it is possible to estimate their effects on the final spectrum by averaging the spectrum for each tautomer according to a Boltzmann distribution (Ref).
An example where tautomeric effects are especially important is urocanic acid, one of the main UV chromophores in our skin. As shown in the figure below, there are two tautomers giving important contributions to the total spectrum.
![Simulated and experimental UV spectra of urocanic acid. The two most relevant spectral contribution from two tautomers are also shown.[66]](https://barbatti.org/wp-content/uploads/2014/05/ua_spect.jpg?w=620)
Simulated and experimental UV spectra of urocanic acid. The two most relevant spectral contribution from two tautomers are also shown (Ref).
1 Comment
Absorption and Fluorescence Spectra of PPV Oligomers | Light and Molecules · November 28, 2014 at 9:09 AM
[…] UV/Vis spectrum simulations […]