On-the-fly Dynamics of Transient Anions

A new method allows simulating transient anions dynamics with mixed quantum-classical techniques.

In brief:

A novel method for simulating dynamics of dissociative electron attachment (DEA) is presented:
- Resonance energies are computed with electron scattering calculations for few geometries; this information is used to parametrize a phenomenological model for the resonance energy.
- An ensemble of classical trajectories for the anion is propagated on-the-fly; the probability of electron autodetachment is simultaneously calculated.
- DEA crosssection is calculated from a nuclear ensemble built out of the results of the dynamics.
The method allows calculating DEA crosssection for general molecules, including all nuclear degrees of freedom, and without pre-computed potential energy surfaces.

Among electron-induced processes in molecular systems, dissociative electron attachment (DEA) plays a prominent role in biological, cold-plasma, material, and environmental sciences.

The process we are interested in is the following: a transient anion AB^– is formed when a low-energy electron is captured by a molecule AB,

e^– + AB → AB^–

Then, the transient anion may either undergo a molecular fragmentation through DEA

(1) A + B^– (DEA)

or lose the electron back to the environment through autodetachment

(2) AB + e^– (autodetachment)

In spite of its significance as a fundamental physicochemical process, and its relevance to several fields, theoretical attempts to describe the dynamics of the transient anions are still limited to low-dimensionality systems.

In a project led by Fabris Kossoski, we propose a novel theoretical framework for describing the dynamics of the competition between DEA and autodetachment [1]. The basic idea of our computational strategy is to classically propagate nuclei on potential energy surfaces computed on-the-fly with bound-state methods.

At each time step, the probability of electron autodetachment is evaluated with a phenomenological model built from electron scattering calculations for a few selected nuclear geometries. Thus, we should be able to simulate DEA, including all nuclear degrees of freedom and without requiring pre-computed potential energy surfaces.

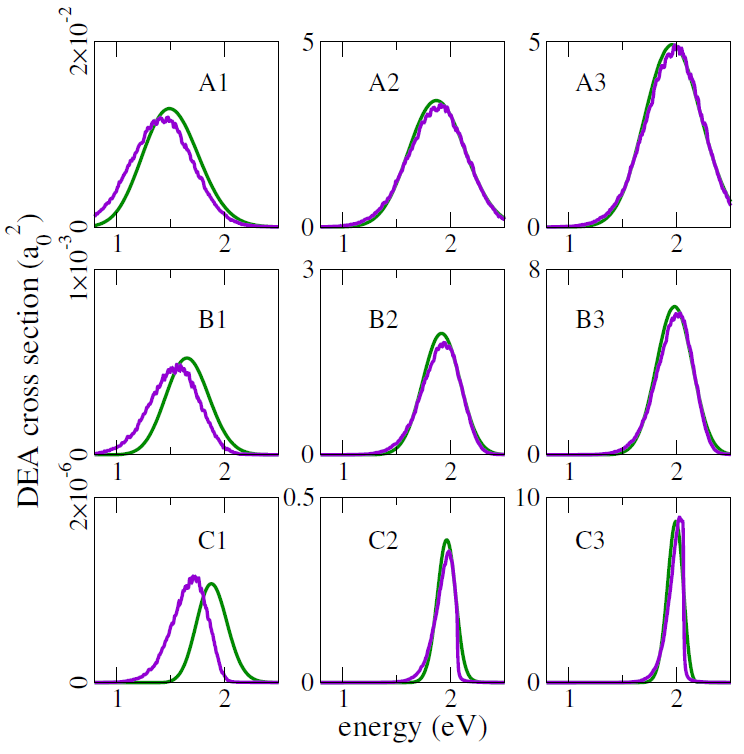
This mixed quantum-classical (MQC) dynamics approach was benchmarked against full quantum dynamics propagations, for one-dimensional potential energy models. Different slopes of the dissociating curve, resonance widths, temperatures, and reduced masses were considered, and both methodologies consistently delivered quite close DEA cross-sections, as shown in the figure below (green curves: quantum results; purple curves: MQC results).

Note in particular that the crosssections in these benchmark evaluations span four orders of magnitude!

As a first multidimensional application, we considered the electron-induced dissociation of chloroethane (CH₂CHCl). The simulated DEA crosssection is shown in the figure below computed from 1000 trajectories (solid purple curve) and from 100 trajectories (dashed purple curve) and compared to the experimental crosssection (red curve). The MQC method delivered results in a semi-quantitative agreement with the experiments.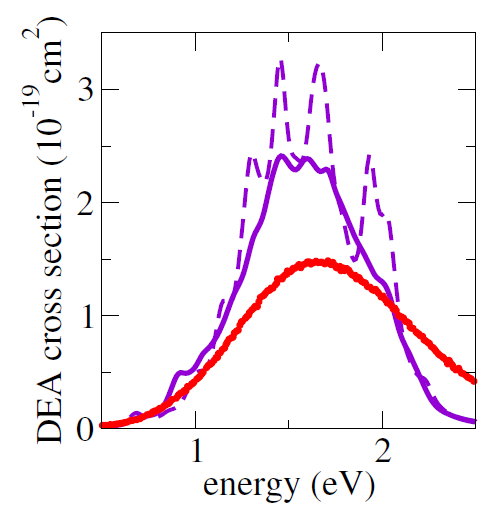

The new method has been implemented into Newton-X and will be freely available to the community in the next release of the code.

Resonance energy, survival probability, and crosssection

The description of the transient anion is the tricky part of the method.

Different from conventional bound-states normally used in computational chemistry, the transient anion is coupled to the continuum and has a complex-valued potential energy

E = E_r − iΓ/2

where E_r is the resonance energy relative to the neutral state, and Γ is the local resonance width, which controls the autodetachment rate.

To get Γ, we’ve done scattering calculations with the Schwinger multichannel method with pseudopotentials for a few points along the potential energy profile of the dissociating anion. Γ(q) obtained for these few geometries is interpolated to get a Γ(E_r) function, which is used to estimate the resonance energy for each point during the dynamics.

This procedure renders Γ(t), which can be integrated to deliver the survival probability P_surv during the dynamics

P_surv =exp( -∫^tΓ(t’) dt‘ )

(P_surv is the probability that electron autodetachment has not taken place until time t for an initial condition x = (q₀,p₀) sampled from a distribution W.)

Finally, the DEA crosssection

σ(E) = π/E ∫ Γ(q₀,E) δ(E−E_r) P_surv(x) W(x) dx

is evaluated with the nuclear ensemble approach, summing over all trajectories.

Reference

[1] F. Kossoski, M. T. do N. Varella, and M. Barbatti, On-the-Fly Dynamics Simulations of Transient Anions, J. Chem. Phys. 151, 224104 (2019).