Interface between Newton-X, DFTB+, and TheoDORE enables nonadiabatic dynamics at nanoscale.
In brief:
- Surface hopping dynamics based on linear-response TD-DFTB is implemented in Newton-X.
- Advanced analysis of transition densities during dynamics is implemented as well.
- Dynamics of cycloparaphenylenes is investigated as a test case.
- Benchmarks for TD-GGA-DFTB, TD-LC-DFTB, and single-determinant SD-DFTB are delivered.
Nonadiabatic processes upon photoactivation are an essential operation feature of many nanostructured materials, as those used for photonic and photovoltaic devices. Nevertheless, the simulation of the time-dependent evolution of the electronic densities in these systems is still a major challenge for quantum chemistry due to their large scale, usually assembling hundreds of atoms in the optically active region.
In the last years, excited-state simulations based on single-determinant (SD) DFT approaches was popularized as an inexpensive way to probe nonadiabatic dynamics in nanostructured materials. In SD-DFT, each excited state is modeled by single Kohn-Sham determinant and its energy is given by the difference between Kohn-Sham orbital eigenvalues. Nevertheless, SD-DFT may be too crude to capture the complexity of the excited-state densities.
An option to enable affordable electronic structure calculations beyond SD-DFT is to use the time-dependent linear response based on a semiempirical approximation to DFT called density functional tight binding (DFTB).
In DFTB, the total energy is derived employing a minimal basis set of localized atomic orbitals, obtained by solving the DFT equations for isolated atoms. Moreover, orbital overlaps and certain Hamiltonian matrix elements are parameterized based on DFT calculations. Higher-level approximations are obtained by performing a Volterra expansion of the Kohn-Sham DFT total energy functional around a reference electronic density to second order (DFTB2) or third order (DFTB3). This range of approximations renders a hierarchy of methods that may be three orders of magnitude faster than DFT.
Excited states within DFTB can be computed following the same formalisms as in DFT, such as the linear-response (LR) time-dependent (TD) approach, that is TD-DFTB; or even the single-determinant version, SD-DFTB.
In a project led by Ljiljana Stojanović, we have implemented an algorithm for fewest switches surface hopping with simplified decay of mixing (SDM-FSSH) based on (LR) TD-DFTB electronic structure. The method is still enhanced by advanced transition density analysis. Approximations up to DFTB3 including empirical dispersion corrections (+D3), nuclear ensemble spectra, local diabatization, and overlap-based nonadiabatic couplings (either using determinants or orbitals) are available. The implementation involves an interface between Newton-X for couplings and dynamics, DFTB+ for TD-DFTB calculations, and TheoDORE for transition density analysis.
The SDM-FSSH (LR) TD-DFTB dynamics has been tested for the gas-phase relaxation of two cycloparaphenylenes, [8]CPP and [10]CPP. It helped to explain some important features of the nonadiabatic dynamics of these molecules, such as the origin of their long fluorescence lifetimes (related to the slow radiative emission from the S1 state) and the trend of increasing the fluorescence rate with the molecular size (related to an increase in the S1-S0 energy gaps and oscillator strengths in the larger molecule).
The quality of the TD-DFTB electronic structure information during dynamics was accessed through four descriptors:
- Excitation energies (ΔE);
- Charge-transfer (CT), which estimates the charge-transfer character of states;
- Participation ratio (PR), which tells the degree of delocalization of the electronic density; and
- Participation ratio of natural transition orbitals (PRNTO), which estimates the multiconfigurational character of the states.
These four quantities were computed during dynamics and recomputed for the same geometries with the higher level long-range corrected TD-LC-DFTB and the lower level SD-DFTB. Distributions of ΔE, PR, and PRNTO are shown in the figure below.
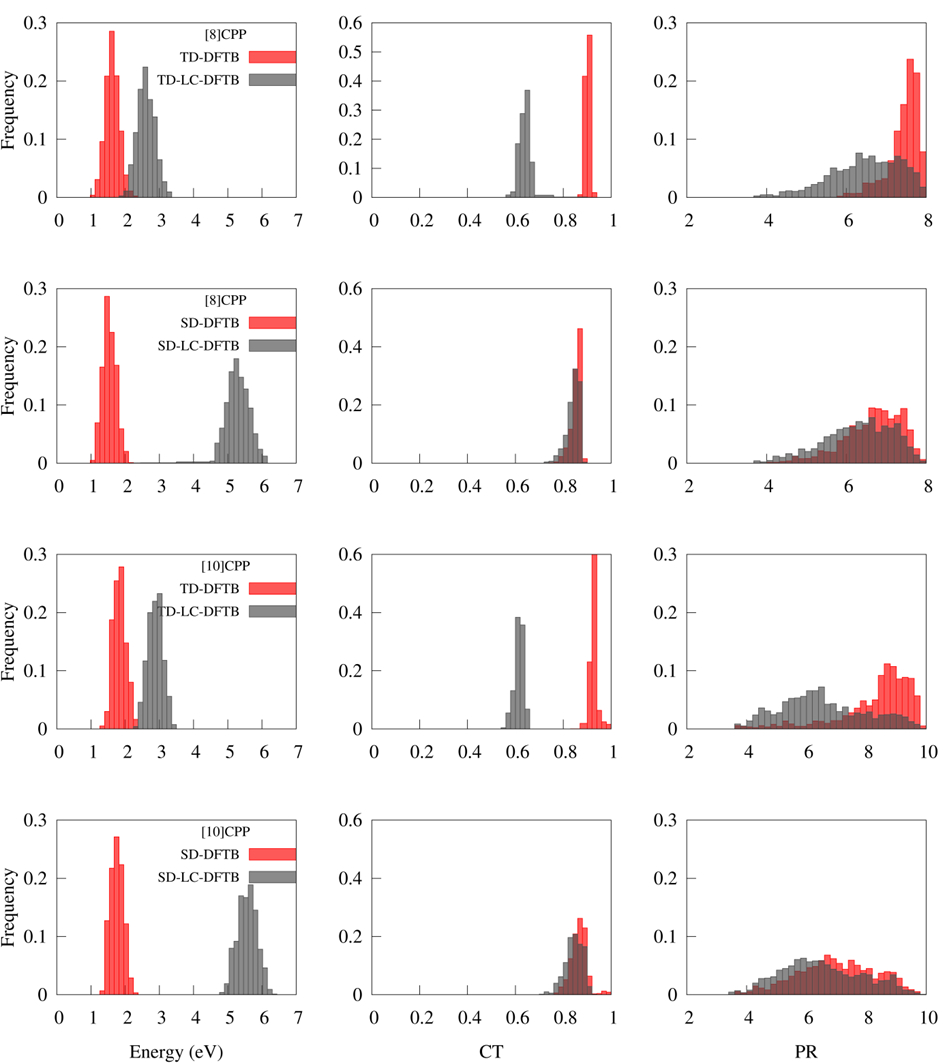
Distributions of ΔE, CT, and PR for [8]CPP and [10]CPP computed with TD-DFTB, TD-LC-DFTB, SD-DFTB, and SD-LC-DFTB, for geometries accessed during TD-DFTB dynamics in the first excited state (3 ps).
In summary:
- TD-DFTB based on a GGA functional enables nonadiabatic dynamics for scales that we cannot reach with TD-DFT. But it must be used carefully, as it may deliver qualitatively wrong results, especially if charge-transfer states are involved. (The same is true for TD-DFT based on GGA functionals anyway.)
- TD-DFTB based on range-separated functionals is a good alternative, but dynamics is still not possible due to the lack of analytical gradients. (This feature is under development and it will be available in the near future.)
- SD-DFTB shows the same problems as TD-DFTB with GGA functionals. LC corrections in this case not only doesn’t lead to any improvement but they may even degrade the results.
These results have been published in a recent issue of JCTC [1].
The SDM-FSSH TD-DFTB algorithm will be soon released in a new version of Newton-X.
MB
Reference
[1] Ljiljana Stojanović, Saadullah G. Aziz, Rifaat H. Hilal, Felix Plasser, Thomas A. Niehaus, and Mario Barbatti, Nonadiabatic dynamics of cycloparaphenylenes with TD-DFTB surface hopping, J. Chem. Theory Comp. doi: 10.1021/acs.jctc.7b01000 (2017).