Meldruns photophysics follows a two-step logistic decay through a charge-transfer state.
In brief:
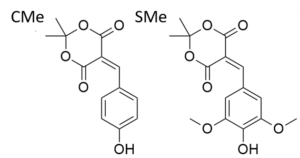
- We simulated the excited-state dynamics of coumaryl Meldrum (CMe) and sinapoyl Meldrum (SMe).
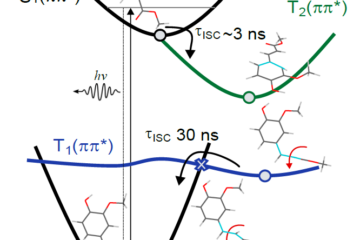
- Both molecules undergo sub-picosecond decay to the ground state through a two-step process involving a twisted intramolecular charge-transfer excited state.
- The two-step decay follows a logistic model, rendering a sigmoid population evolution.
Skin photoprotection against UVA radiation is crucial, but it is hindered by the sparsity of approved commercial UVA filters. Sinapoyl malate (SM) derivatives are promising candidates for a new class of UVA filters. They have been previously identified as efficient photoprotective sunscreen in plants due to their fast nonradiative energy dissipation.
Combining experimental and computational results, the BoostCrop consortium has recently shown that coumaryl Meldrum (CMe) and sinapoyl Meldrum (SMe) are outstanding candidates for UVA filters in sunscreen formulations.
In this new work, led by Josene Toldo, we deliver a comprehensive computational characterization of the excited-state dynamics of CMe and SMe. Using reaction pathways and excited-state dynamics simulations, we could elucidate the photodeactivation mechanism of these molecules.
Upon photoexcitation, they follow a two-step decay:
- First, an ultrafast and efficient relaxation stabilizes the excited state alongside a 90º twisting around the allylic double bond, giving rise to a minimum with a twisted intramolecular charge-transfer (TICT) excited state character.
- From this minimum, internal conversion to the ground state occurs after overcoming a 0.2 eV barrier.
Minor differences in the nonradiative decay and fluorescence of CMe and SMe are associated with an additional minimum present only in the latter.
Logistic photophysics
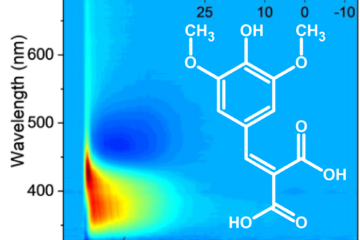
One outstanding feature of the two-step decay of these molecules is that their excited-state population has a sigmoid shape
p\left( t \right)=\frac{a}{1+\exp \left( \frac{t-{{\tau }_{L}}}{{{\tau }_{E}}} \right)}This sigmoid shape implies that the dynamics is governed by a logistic model, and as such, the exponential decay to the ground state depends on the accumulation of a critical population in an intermediate excited state species.
First, an intermediate excited-state species must be formed within \tau_L, and then the ground state is exponentially populated from this intermediate population within \tau_E. a is the total variation of the population. The internal conversion lifetime, corresponding to the time to reduce the excited-state occupation to 1/e, is
{{\tau }_{IC}}\equiv {{\tau }_{E}}\ln \left( e-1 \right)+{{\tau }_{L}}We believe that logistic decay may be a common feature in molecular photophysics that has been overlooked in previous works.
MB
Reference
[1] J. M. Toldo, M. T. do Casal, M. Barbatti, Mechanistic Aspects of the Photophysics of UVA Filters Based on Meldrum Derivatives, J. Phys. Chem. A, DOI: 10.1021/acs.jpca.1c03315 (2021).