Simple proxies can predict diabatic and nonadiabatic couplings.
In brief:
- SEIC is a general class of reactions having singlet fission and triplet fusion as particular cases.
- For these reactions, we show that:
- diabatic couplings are proportional to orbital overlaps.
- nonadiabatic couplings can be approximated by the CT coefficients in the wave function.
Spin-exchange internal conversion (SEIC) forms a class of reactions where the global spin of a molecular complex A – B is conserved, while the spin of the monomers A and B is changed. The most famous example of such a reaction is the singlet fission (SF):
(1) 1[1A + 1B] → 1[3A + 3B]
Another example of SEIC is the triplet fusion reaction (TF):
(2) 1[3A + 3B] → 1[1A + 1B]
A practical occurrence of reaction (2) is in the singlet-oxygen photosensitization.
In the literature, SEIC reactions have been treated either in the diabatic or in the adiabatic representation.
In this work [1], Shuming and I went deep in the SEIC mechanism in both representations to derive proxies for the diabatic and nonadiabatic couplings. These couplings are needed to estimate the SEIC reaction rate.
Although diabatic and nonadiabatic couplings can be in principle computed from first principles, many of the supra-molecular systems showing SEIC are in the materials science field and having inexpensive ways of estimating the couplings could be of great help.
In the diabatic representation, if the SEIC reaction is mediated by a charge-transfer (CT) state, we show that the diabatic coupling (V) can be written as
(3) V = η <φA|φB><φ’B|φ’A>
where <φA|φB> is the overlap between the two frontier molecular orbitals in each monomer. In our tests, we assumed η to be a simple proportionality constant.
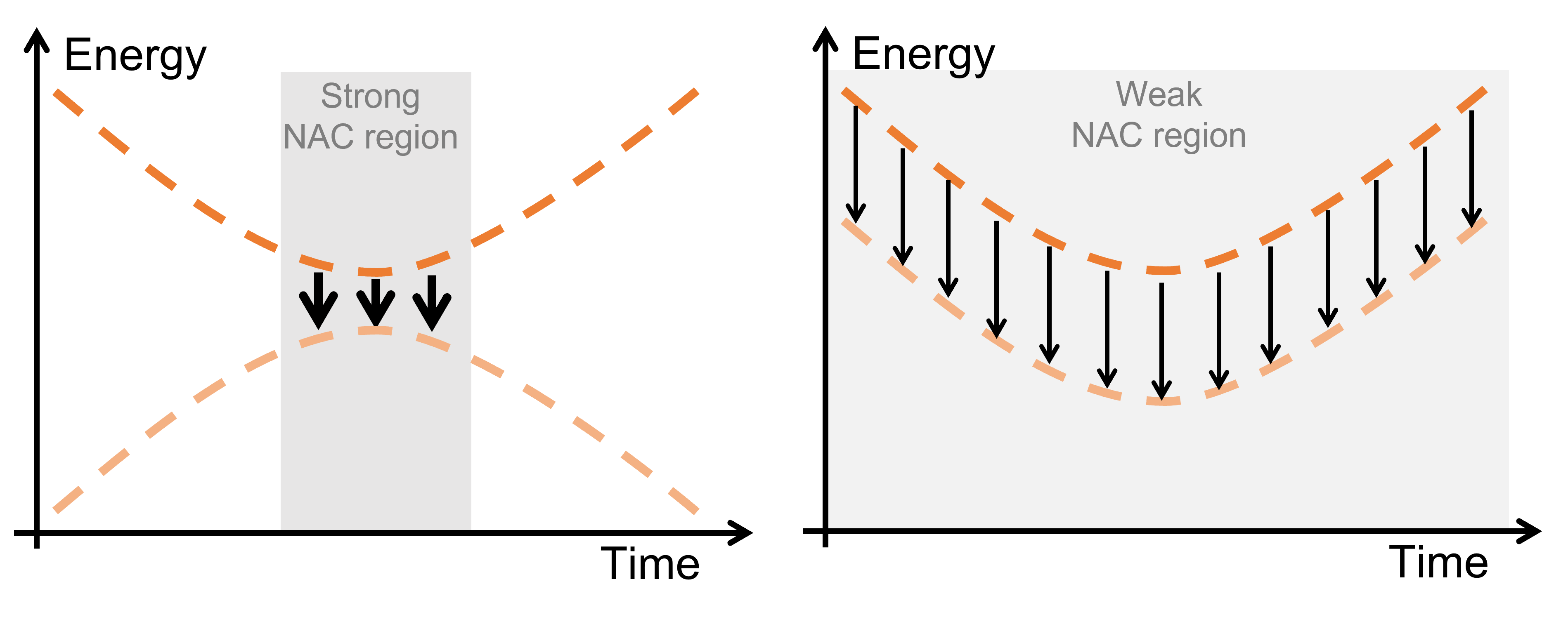
In the adiabatic representation, we show that the nonadiabatic coupling (F) in the SEIC reaction is
(4) F = γ κCT
where γ groups the terms dependent on energies and energy derivatives and
(5) κCT = Σi∈CT ci(1)ci(2)
where ci(n) is the CI coefficient of the CT configurations in state n.
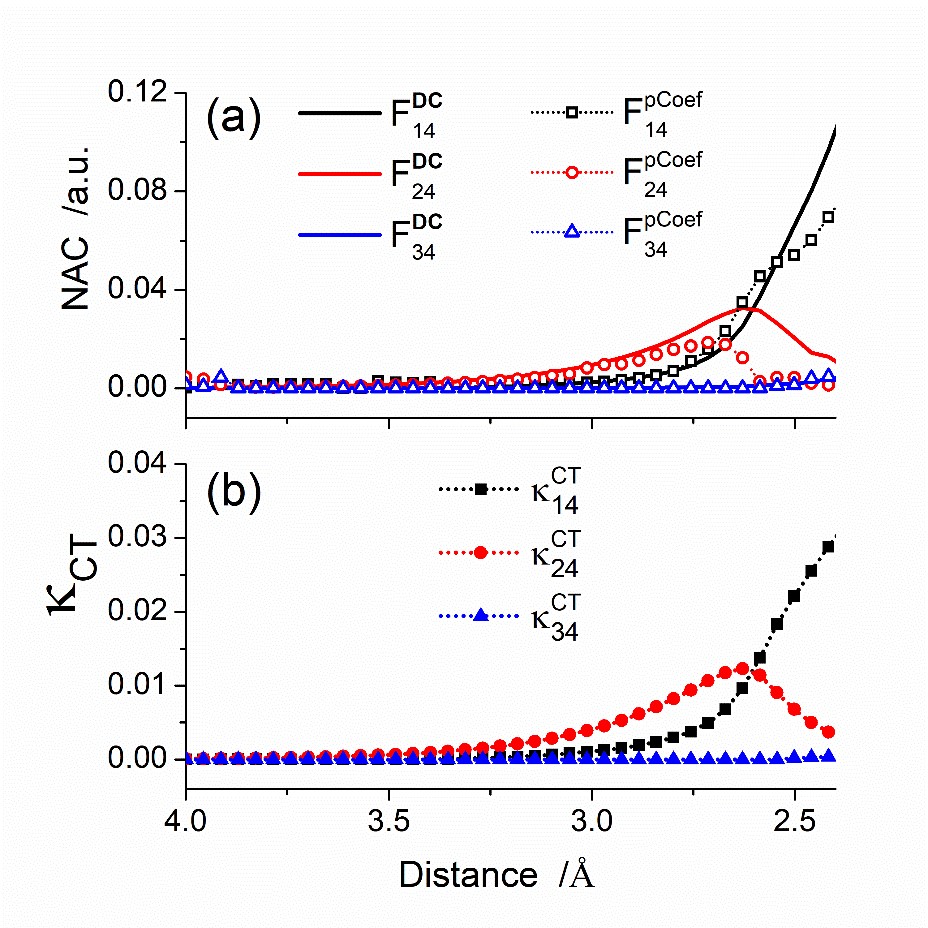
We have tested these proxies for V and F for a PS – O2 reaction, taking PS as a thiothymine photosensitizer. The figure below, for instance, shows fully computed nonadiabatic couplings (top) and the corresponding proxy values (bottom) for a particular PS – O2 collision direction. The agreement is excellent.
The new proxies in the adiabatic and diabatic representations have their own advantages.
The nonadiabatic proxies are obtained based on quantum chemical calculations and provide robust results comparable to the full NAC strength.
On the other hand, the orbital overlaps in the diabatic representation are easier to analyze even without resorting to explicit calculations. In the example studied in our paper, just the shapes of four key MOs were enough to deliver a qualitative analysis.
These results are discussed in Ref. [1].
MB
Reference
[1] S. Bai and M. Barbatti, Mechanism of Spin-Exchange Internal Conversion: Practical Proxies for Diabatic and
Nonadiabatic Couplings, J. Chem. Theory Comp. DOI: 10.1021/acs.jctc.8b00923 (2019).