A Kinetic Model for Singlet Oxygen Photogeneration

Reaction rates for energy transfer in floppy complexes calculated from first principles.

For decades, photosensitizers (PS) for singlet oxygen (¹O₂) generation have been developed for applications in chemical synthesis and phototherapy. In the most relevant channel in solution, it takes place through the reaction

¹[³PS+³O₂] → ¹[¹PS+¹O₂],        (1)

in which a singlet complex (with each monomer in the triplet state) undergoes internal conversion to another singlet state of the complex (but now with the monomers also in the singlet state).

Computational theoretical chemistry has been quite timid in the treatment of such process due to the difficulties related to the underlying intermolecular energy-transfer problem, the floppy nature of the PS-O₂ complex, and the open-shell character of the system.

Shuming Bai and I have been working on a research program to face this challenge. Step by step, we have built the basis to calculate the reaction rates for Reaction (1). Taking thiothymines as a prototypical PS, we started by explaining their absorption spectroscopy and formation of the triplet PS; then, we showed how the triplet PS can be lost before interacting with oxygen. In our most recent work, we address the how to compute reaction rates [1].

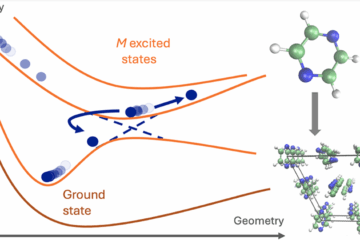
To compute such rates, we developed a model named Divide to Conquer (DtC). The model is an extension of the Marcus theory for the inverted region, from parabolic potential curves to parabolic sheets, as illustrated in the figure below. Such additional dimension D, corresponding to the intermolecular coordinate between PS and O₂, should be taken into account due to the fact that, first,  the complex does not form rigid structures and, second, D does not contribute to the crossing between the initial and final states. This crossing occurs along the intramolecular coordinates R of PS.

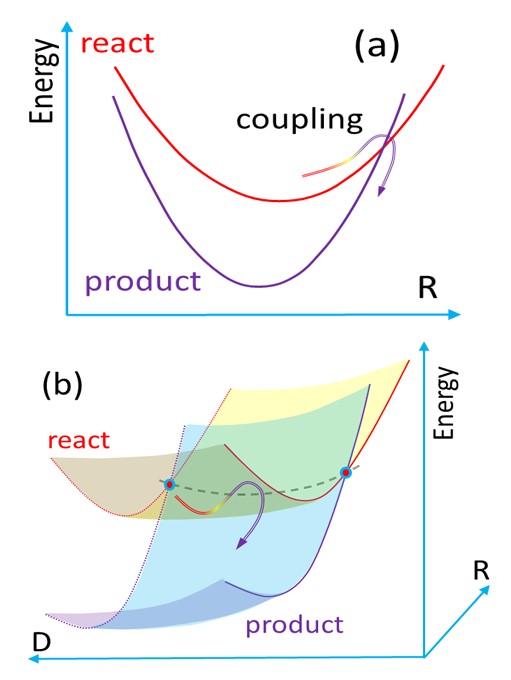
(a) Potential energy profile for the conventional Marcus model. (b) Extended surfaces for the Divide-to-Conquer model.

Under the hypothesis that the interaction energy between the monomers mainly depends on D, we showed that the quantities needed to calculate the rate as a function of D—the activation energy, the reorganization energy, and the diabatic coupling—-can all be obtained by a minimum set of routine quantum chemical calculations involving:

• determination of the triplet state minimum for the isolated PS;
• determination of the triplet/singlet crossing point for the isolated PS;
• calculation of the rigid energy profile between these two geometries;
• calculation of a rigid energy profile (and nonadiabatic couplings) along D for the frozen PS-O₂ complex.

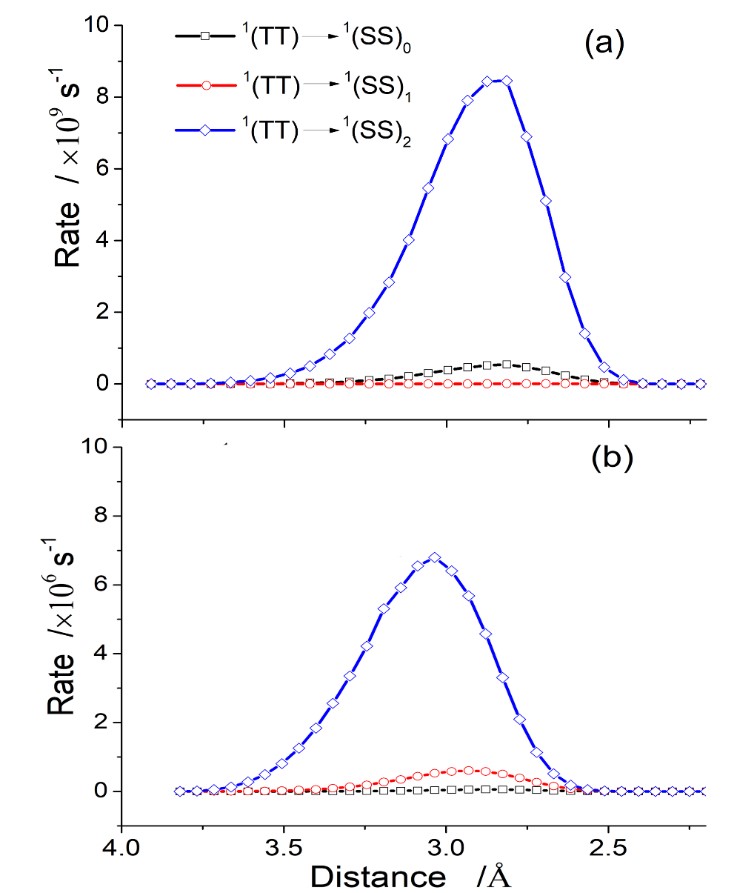
These quantities are all we need to feed the DtC model, which directly delivers the rates for Reaction (1) as a function of D, as shown in the figure below for two different PS-O₂ incidence directions.

Reaction rates to form singlet oxygen for two different PS-O₂ incidence directions.

Applying the DtC model to study singlet oxygen photosensitized by 6-aza-2-thiothymine, we learned that there is a strong dependence of the reaction rate on the PS-O₂ incidence directions and final electronic states. Rates for different directions may differ by a factor 1000. Independently of direction, the singlet oxygen yield in the ¹Σ_g state exceeds that in the ¹Δ_g state by a factor 10.

MB

Reference

[1] Shuming Bai and Mario Barbatti, Divide to Conquer: A Kinetic Model for Singlet Oxygen Photosensitization, J. Chem. Theor. Comp. doi: 10.1021/acs.jctc.7b00619 (2017). (50 free copies)

To know more

• On the decay of the triplet state of thionucleobases
• Explaining the photophysics of thiothymines
• Revisiting the excited-state dynamics of thymine