Wigner distribution or ground-state trajectories, what is the best way to sample initial conditions for excited-state dynamics?
In diverse types of simulations, one needs to sample nuclear conformations of a molecule considering the kinetic energy deposited in the internal vibrational modes. This is the case, for instance, of the sampling of the phase space (geometries and velocities) to initiate excited-state dynamics or the sampling of the configurational space (geometries only) for spectrum simulations.
There are two basic approaches to carry out these samplings: one may either sample the space by considering that the molecule is at its zero-point energy level (quantum or Q sampling); or, alternatively, one may sample the space supposing that the molecule is in thermal equilibrium with the environment (thermal or T sampling).
In practical terms, the Q sampling is done picking coordinates from a mutidimensional Gaussian distribution, while in the T sampling, the coordinates are picked from trajectory simulations.
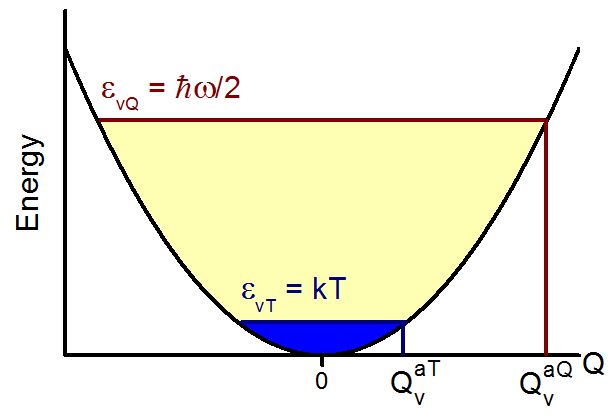
Although we can find examples of both approaches in the literature, they are far from equivalent. While in the Q sampling each vibrational degree of freedom j has energy ħωj/2, in the T sampling each degree has kT. Because at T = 300 K, ħωj/2 (~0.1 eV) is much larger than kT (~0.03 eV), the vibrational amplitudes in the Q sampling are much larger than in the T sampling, as illustrated for one dimension in the figure below. This also means that simulations based on one or other approach may render different results.
In a recent research project [1], Kakali Sen and I investigated the effects of using these different types of samplings on the absorption spectrum and excited-state dynamics. We took pyrrole as test case, computing spectra with the nuclear ensemble approach and dynamics with surface hopping. ADC(2) was used for the electronic structure calculations.
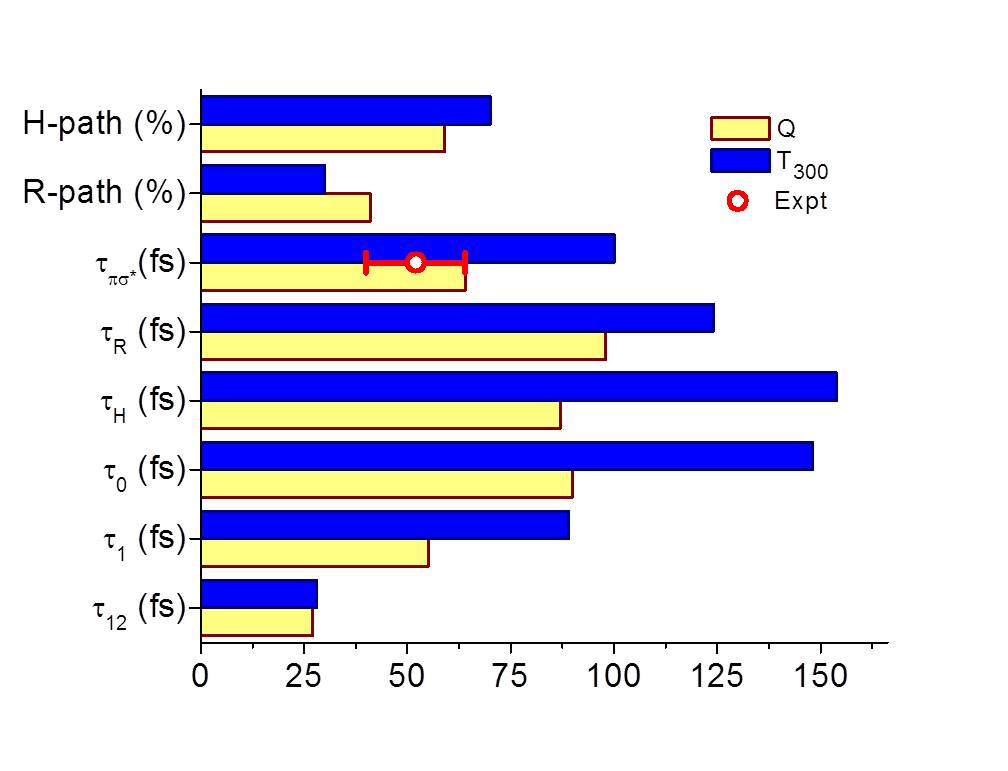
The results are quite clear: T samplings systematically delivered too narrow spectra and too slow dynamics compared to the Q sampling and to the experiments. Thus, the Q sampling is the most consistent way to generate initial conditions.
 The reason for the superiority of the Q sampling may be understood by checking the next figure. The graphs at left show the distribution of ground-state kinetic and total energies in the ensemble of nuclear geometries computed with different sampling methods. The graphs at right show the distribution of specific coordinates in the ensembles.
The reason for the superiority of the Q sampling may be understood by checking the next figure. The graphs at left show the distribution of ground-state kinetic and total energies in the ensemble of nuclear geometries computed with different sampling methods. The graphs at right show the distribution of specific coordinates in the ensembles.
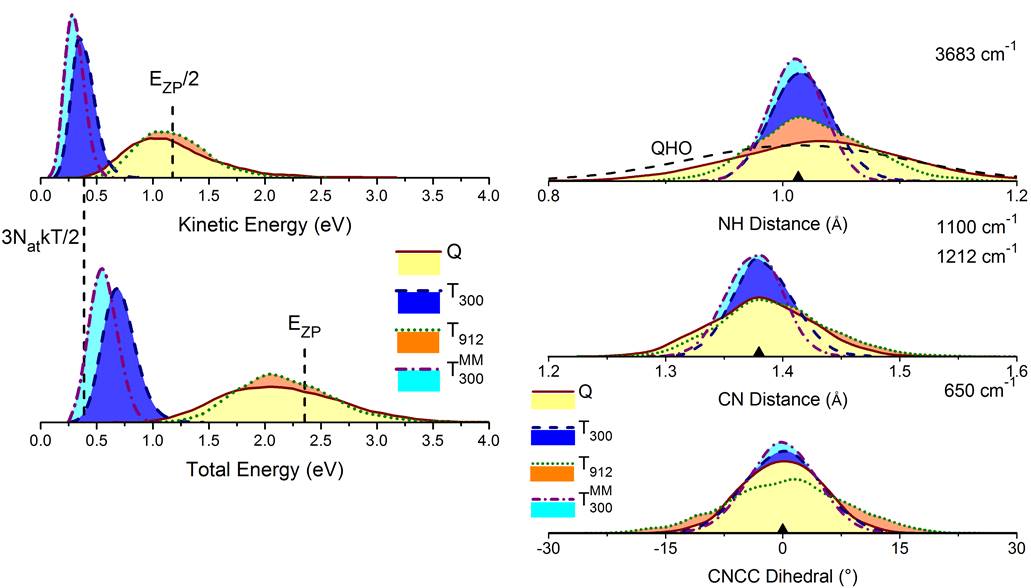 The differences between T and Q sampling distributions are striking, with Q always corresponding better to what we would expect to be the true distribution of a quantum system.
The differences between T and Q sampling distributions are striking, with Q always corresponding better to what we would expect to be the true distribution of a quantum system.
This is a short overview of the work, which in fact contains quite a lot of more information on sampling methods. We analyze what happens when we overheat the T sampling till it reaches the zero-point energy; we check whether there are differences between doing a T sampling using Born-Oppenheimer or Molecular-Mechanics; we discuss what to do when we cannot directly apply a Q sampling, as in QM/MM simulations.
As a side product, the paper also brings a fresh batch of dynamics simulations for pyrrole in the gas phase.
Reference
M. Barbatti and K. Sen, Effects of different initial condition samplings on photodynamics and spectrum of pyrrole, Int. J. Quantum Chem., doi:10.1002/qua.25049 (2015).