Legion: A New Platform for Gaussian Wavepacket Dynamics

A new software for multiple spawning in the Newton-X framework.

What happens when a molecule absorbs light? In a fraction of a second, electrons jump, nuclei shake, and new chemical paths open up. Understanding this excited-state dance is crucial for fields like photochemistry, materials science, and biological processes.

Simulating these ultrafast processes is a challenge our group has been tackling for years. On one side, we have highly accurate quantum methods, like MCTDH, but they are computationally expensive. On the other, mixed quantum-classical trajectory-based approaches, like surface hopping, are faster but introduce strong approximations. Somewhere in between, Gaussian wavepacket methods, such as ab initio multiple spawning (AIMS), promise a balance between speed and precision.

That’s where Legion comes in.

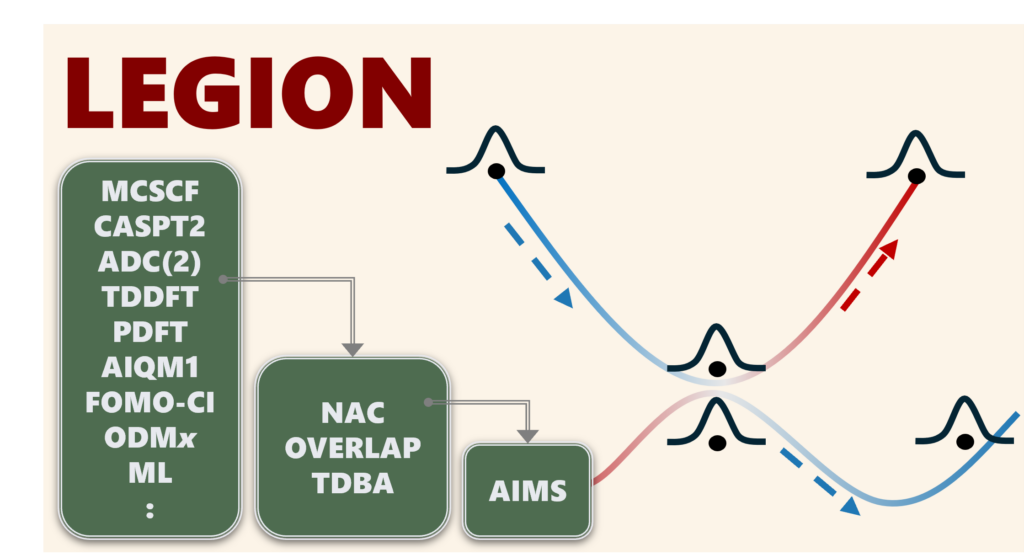
Legion is a new software program Rafael S. Mattos designed for Gaussian wavepacket nonadiabatic dynamics. The first version focuses on the AIMS method, where a swarm of classical trajectories is used to construct quantum wavepackets that evolve following Schrödinger’s equation. When the system reaches regions of strong electronic interaction, new trajectories spawn, capturing the quantum effects of population transfer between electronic states.

Rafael built Legion under the Newton-X platform to automatically gain access to a wide range of electronic structure interfaces, from semiempirical methods (like OM2/MRCI) to high-level methods (like CASPT2 and MRCI). Unlike existing options, Legion provides a flexible approach to nonadiabatic couplings, allowing simulations even when explicit coupling vectors are unavailable. It also enables dynamics with atoms across the entire periodic table.

To keep calculations efficient, Legion counts on several approximations and numerical techniques:

• Bra-Ket Averaged Taylor/Exponential (BATE) Approximation: A new way to estimate nonadiabatic couplings without computing additional electronic structure points.
• Time-Dependent Baeck-An Coupling (TDBA): A method that avoids the direct computation of electronic wavefunction overlaps, expanding the range of applicable quantum chemistry methods. You can still use conventional NAC vectors if you prefer. However, TDBA enables dynamics with any electronic structure technique, including, for example, TDDFT.
• Adaptive Timesteps: A strategy that refines step size only when needed, improving efficiency without losing accuracy.

We tested and validated Legion on two well-known photochemical systems, fulvene and DMABN, molecules that serve as molecular analogs of Tully’s famous nonadiabatic test cases. Legion successfully reproduced known excited-state dynamics using multiple electronic structure methods (TDDFT, CASSCF, CASPT2), confirming its accuracy.

One of the most exciting tests was running TDDFT-based AIMS without nonadiabatic coupling vectors, which was made possible through the TDBA approximation. This expands the range of methods available for quantum dynamics simulations.

This is just the beginning. Legion’s modular design means new methods can be implemented easily. Future developments will include train-of-trajectories techniques, a more robust variational propagator, and even more flexible nonadiabatic coupling strategies.

Legion is open-source and freely available, making AIMS simulations more accessible.

Check out Legion here: GitLab Link. The reference to the paper describing Legion in detail is below.

MB

Reference

[1] R. S. Mattos, S. Mukherjee, M. Barbatti, Legion: A Platform for Gaussian Wavepacket Nonadiabatic Dynamics, J. Chem. Theory Comp. (2025). DOI: 10.1021/acs.jctc.4c01697