Ultrafast internal conversion without energy crossing

Theory shows conditions for having sub-ps lifetime without conical intersections.

Consider these two recent case studies from the literature:

1. Mansour et al. showed with surface hopping simulations that the S₃-state lifetime of protonated azaindole is about 100 fs, even though the energy gap between S₃ and S₂ is always about 0.5 eV. I discussed this specific example here.
2. Aleotti et al. reported ML-MCTDH simulations showing that the S₂→S₁ pyrene dynamic occurs within 100 fs without the molecule ever coming near a crossing point.

These results are counterintuitive. The current paradigm of computational photochemistry states that ultrafast internal conversion should occur near a conical intersection. In this scenario, the molecule is in a zero coupling region until it enters a strong coupling region and immediately jumps to another state (right panel below).

However, if there’s no energy crossing, how can the molecule have an ultrafast decay? Doesn’t the Gap Law prescribe that the lifetime gets longer for bigger energy gaps?

Saikat Mukherjee and I proposed that ultrafast internal conversion can also occur in another scenario. If the molecule enters a region of a relatively large gap, but with non-null coupling, the opportunities for internal conversion are so numerous that it can eventually happen (left panel below).

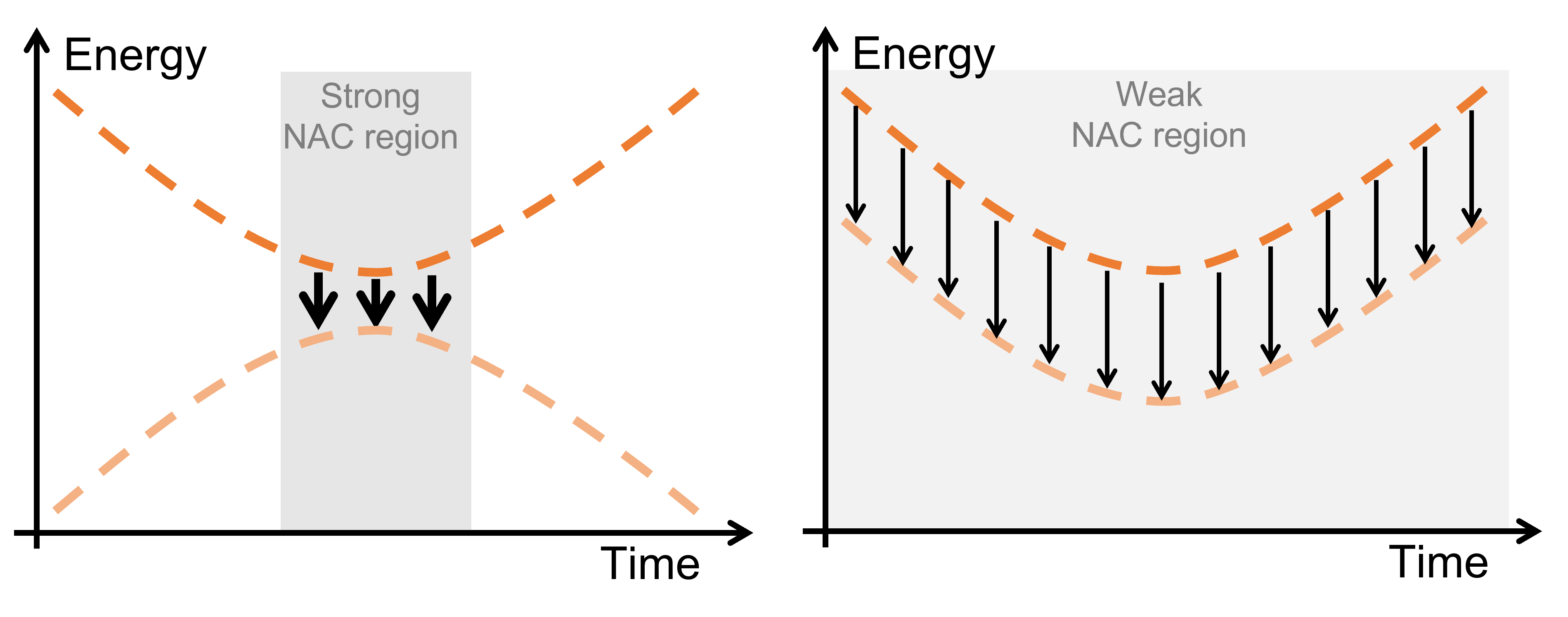
Ultrafast internal conversion can occur in two scenarios: (left) the molecule moves in a region of zero coupling and suddenly finds the strong coupling region near a conical intersection; (right) the molecule moves in a region of weak but non-null coupling, multiplying the opportunities of internal conversion.

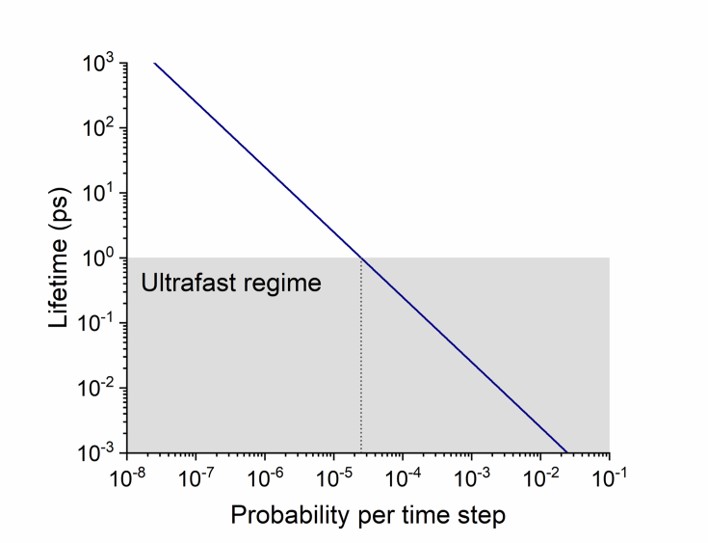
We checked the validity of this weak-coupling scenario with an analytical model. Suppose a molecule in the excited state. It can hop to the ground state with a constant probability p within a time step \Delta t. Suppose yet that, once the molecule is in the ground state, the back hopping probability is zero. In this simple model, we can easily show that the excited-state lifetime is
\tau = -\frac{\Delta t}{ln\left(1-p\right)}.

For a typical time step of 0.025 fs (the default in Newton-X), this equation implies that whenever p is bigger than 2.5 \times 10^{−5}, the lifetime will be under 1 ps.

Excited-state lifetime as a function of the hopping probability for a 0.025 fs time step.

Within 1 ps, the molecule has 1000/0.025 = 40,000 hopping opportunities. Therefore, it isn’t surprising that even with a tiny 0.00001 hopping probability per time step, it still ends up in the ground state.

Let’s go back to the protonated azaindole case. Surface hopping tells that the average S₃→S₂ hopping probability for this molecule is p = 2.4 \times 10^{−4} for \Delta t = 0.025 fs. Taking these values, \tau = 104 fs. (Surface hopping gives 156 ± 40 fs. The difference comes from neglecting back hoppings in the simple analytical model.)

MB

Reference

[1] S. Mukherjee and M. Barbatti. Ultrafast internal conversion without energy crossing, Results Chem 4, 100521 (2022). DOI: 10.1016/j.rechem.2022.100521