Newton-X, G16, and Tinker together for TDDFT/LR-AMOEBA dynamics.
In brief:
- Surface hopping with a TDDFT/MM using a linear-response polarizable embedding approach with the AMOEBA force field is implemented.
- The program interfaces Newton-X NS, Gaussian 16, and Tinker.
- The LR-polarizable approach does not perform significantly better than non-polarizable force fields. State-specific developments are urgent.
Describing solvent effects during nonadiabatic dynamics is one of the biggest challenges in computational photochemistry. Because explicit quantum mechanical (QM) treatment of the solvent molecules is unaffordable, we usually treat solvation via molecular mechanics (MM).
The main problem with the QM/MM approach is that conventional force fields don’t account for solvent polarization due to the excited-state densities. We set the charges representing the solvent at the dynamics input, and they remain constant during the entire simulation.
(However, we consider polarization of the QM region due to the solvent. The solvent charges go into the QM hamiltonian in the so-called electrostatic embedding.)
Polarizable force fields seek to solve this lack of solvent response to the QM densities.
In a collaboration between Mattia Bondanza and Benedetta Mennucci in Pisa and our Baptiste Demoulin and me in Marseille, we implemented trajectory surface hopping nonadiabatic dynamics for a polarizable embedding QM/MM formulation.
TDDFT is used for the QM region, whereas the MM description is done with the AMOEBA polarizable force field. This implementation integrates Newton-X NS with an interface between Gaussian 16 and Tinker to calculate QM/AMOEBA energies and forces within a linear-response (LR) framework.
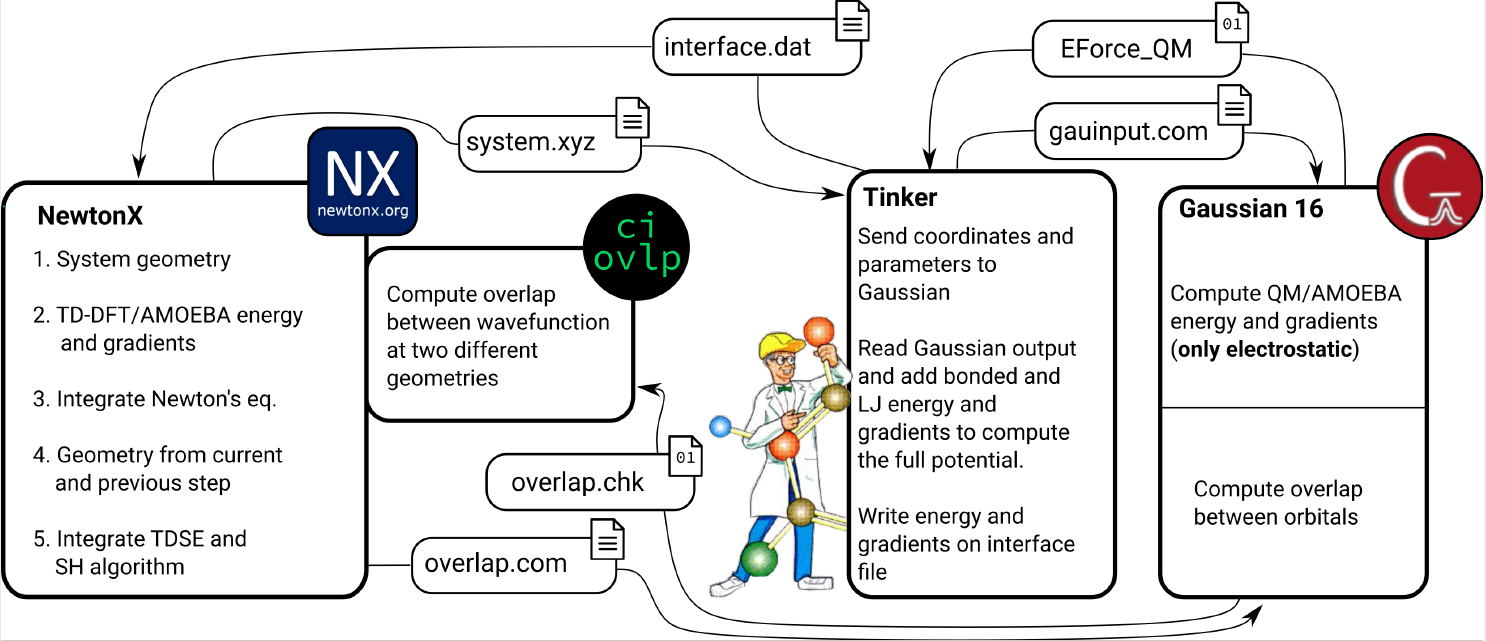
The NX/TINKER/G16 interface will be released under the GPL3 license, freely available to anyone with access to Gaussian 16 and the Tinker version as modified in this work.
We tested our approach on photoexcited pyrimidine-water clusters, a challenging system because of the relevant role played by CT states. We show that the results of AMOEBA (polarizable) and TIP3P (non-polarizable) water models are very similar if AMOEBA is treated in a linear response (see Box 1). Nevertheless, significant differences in the results are obtained when QM/AMOEBA is treated within a state-specific framework (which we can test, but still not do dynamics) or we include the solvent in the QM region.
These findings mean we urgently need reliable and efficient implementations of analytical gradients of state-specific polarizable QM/MM.
Box 1. State-specific x linear-response models
Extending polarizable models to nonadiabatic dynamics is challenging due to the non-linearity introduced into the Hamiltonian caused by the dependence of the polarization degrees of freedom of the environment on the QM charge density. Consequently, different electronic states are eigenfunctions of different non-linear Hamiltonians, and the states aren’t orthogonal to each other anymore.
Thus, implementing surface hopping using a state-specific (SS) environment model is not straightforward. However, if the QM method used for surface hopping simulation is based on a linear-response (LR) formulation, such as TDDFT, the coupling to a polarizable model can be formulated in a much simpler way.
Within LR, the response of the polarizable environment depends on transition densities, not on the charge density of specific states. The resulting response, which is like a dispersion interaction, makes the TD-DFT problem solvable for all the states simultaneously, just like we do for an isolated QM system.
MB
Reference
[1] M. Bondanza, B. Demoulin, F. Lipparini, M. Barbatti, B. Mennucci, Trajectory Surface Hopping for a Polarizable Embedding QM/MM Formulation, J. Phys. Chem. A (2022). DOI: 10.1021/acs.jpca.2c04756
0 Comments