Boltzmann and Gibbs proposed different formulations for statistical physics. Which one is correct?
In brief:
- An analytical approximation for counting microstates of isolated molecules is proposed.
- It’s applied to derive the microcanonical temperature using Boltzmann and Gibbs ensembles.
- It’s shown that these temperatures differ for small molecules, opening a way for testing them experimentally.
- A simple analytical formulation is given to estimate the temperature of isolated molecules.
The enigmatic formula S = k log W is engraved in Ludwig Boltzmann’s tombstone in Vienna, Austria. It commemorates the fundamental proposal of the Austrian physicist that the entropy (S) of a substance is related to its number (W) of microscopic states with the same energy. Boltzmann showed how all other thermodynamic quantities, like temperature, could be derived from this equation, creating the field of statistical physics in the late XIX century.
Relevant as it was, Boltzmann’s formulation is not unique. Josiah Willard Gibbs, another founder of statistical physics, proposed that the entropy should be related not to the number of states with the same energy but to all states up to that energy.
Determining which formulation is correct is crucial for the fundamentals of statistical physics. Moreover, recent experiments proposing negative absolute temperatures have ignited a vigorous Boltzamnn vs. Gibbs debate. Such exotic temperatures (in which a gas of attracting particles does not collapse) are only possible within Boltzmann’s formulation.
I have just developed a theory that can settle the debate. In a recent publication entitled “Defining the temperature of an isolated molecule,” I showed that Boltzmann’s temperature is much higher than Gibbs’s for a molecule with less than ten atoms. Therefore, we can tell who was right, Boltzmann or Gibbs, by measuring the temperature of a small, isolated molecule. I even discuss how such an experiment could be done by monitoring the molecular fluorescence.
My paper also shows that both formulations coincide for larger molecules, explaining why many thermodynamics textbooks mix them, attributing to Boltzmann results from Gibbs’ formulation.
And if you ever need to estimate the temperature of an isolated molecule in a vacuum, here is a simple formula you can use: T={{\left[ \ln \left( \frac{E+{{E}_{ZP}}}{E-{{E}_{ZP}}} \right) \right]}^{-1}}\frac{2{{E}_{ZP}}}{N{{k}_{B}}} , where E is the energy excess, E_{ZP} is the zero-point energy, N is the number of vibrational degrees of freedom, and k_B is the Boltzmann constant.
The temperature of an isolated molecule
The temperature T is related to the entropy S through T={{\left( \frac{\partial S}{\partial E} \right)}^{-1}}.
According to Boltzmann, the entropy is {{S}_{B}}\left( E \right)={{k}_{B}}\ln \left[ \varepsilon \,\omega \left( E \right) \right], where \omega\left( E \right) is the density of microstates with energy E.
Nevertheless, according to Gibbs, the entropy should consider all microstates with energy small or equal to E, {{S}_{G}}\left( E \right)={{k}_{B}}\ln \left[ \Omega \left( E \right) \right]. 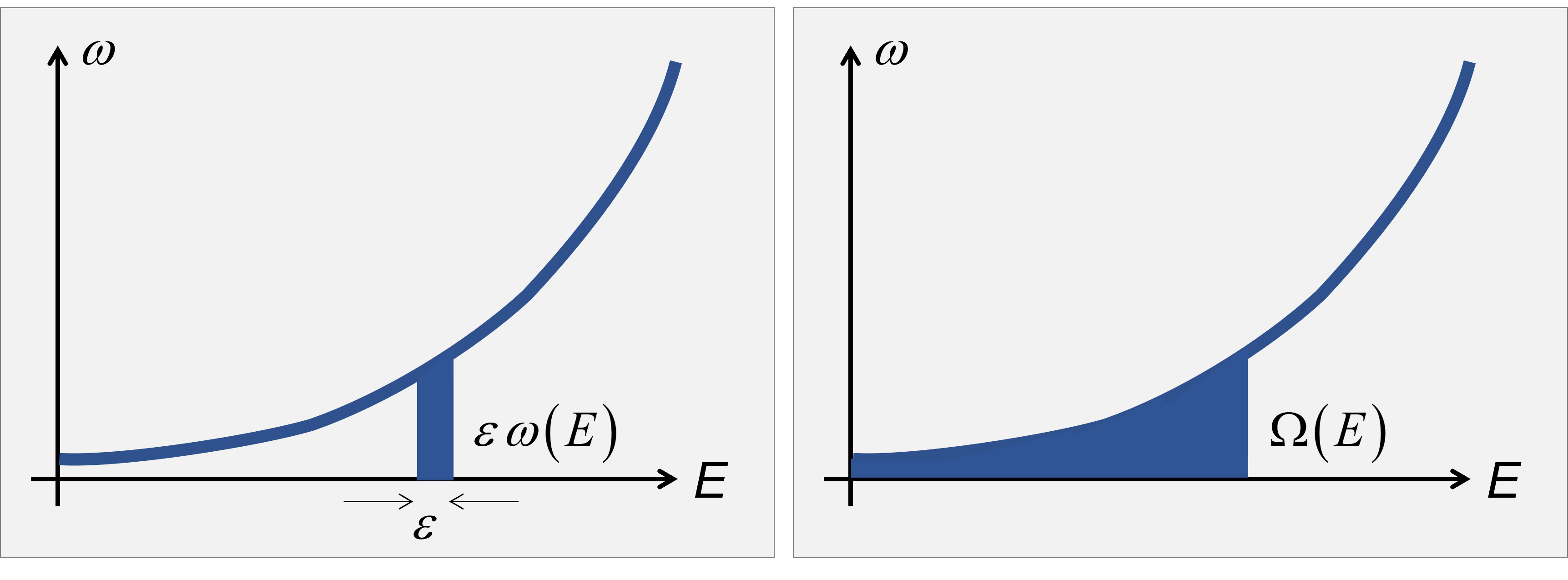 Either way, counting the number of microstates is hard. For an harmonic molecules it means to count how many states the system has between E and E + \varepsilon, or \varepsilon\omega\left(E\right) = \#\left\{ {{E}_{\xi }}={{E}_{ZP}}+\sum\limits_{k}{{{n}_{k}}h{{\nu }_{k}}},\quad {{E}_{\xi }}\in \left[ E,E+\varepsilon \right] \right\}, where \nu_k are the harmonic frequencies.
Either way, counting the number of microstates is hard. For an harmonic molecules it means to count how many states the system has between E and E + \varepsilon, or \varepsilon\omega\left(E\right) = \#\left\{ {{E}_{\xi }}={{E}_{ZP}}+\sum\limits_{k}{{{n}_{k}}h{{\nu }_{k}}},\quad {{E}_{\xi }}\in \left[ E,E+\varepsilon \right] \right\}, where \nu_k are the harmonic frequencies.
In my paper, I show that we can estimate this number by replacing the harmonic frequencies by an average frequency \bar{\nu}. It means \varepsilon\omega\left(E\right) \approx \#\left\{ {{E}_{M}}={{E}_{ZP}}+Mh\bar{\nu},\quad {{E}_{M}}\in \left[ E,E+\varepsilon \right] \right\} . This problem can be solved by combinatorial analysis, allowing to compute the Boltzmann and Gibbs temperatures.
Temperatures calculated using this approximation (I call it the equivalent degenerated model) is within 3% of the exact harmonic temperatures and should be an upper bound to the anharmonic ones.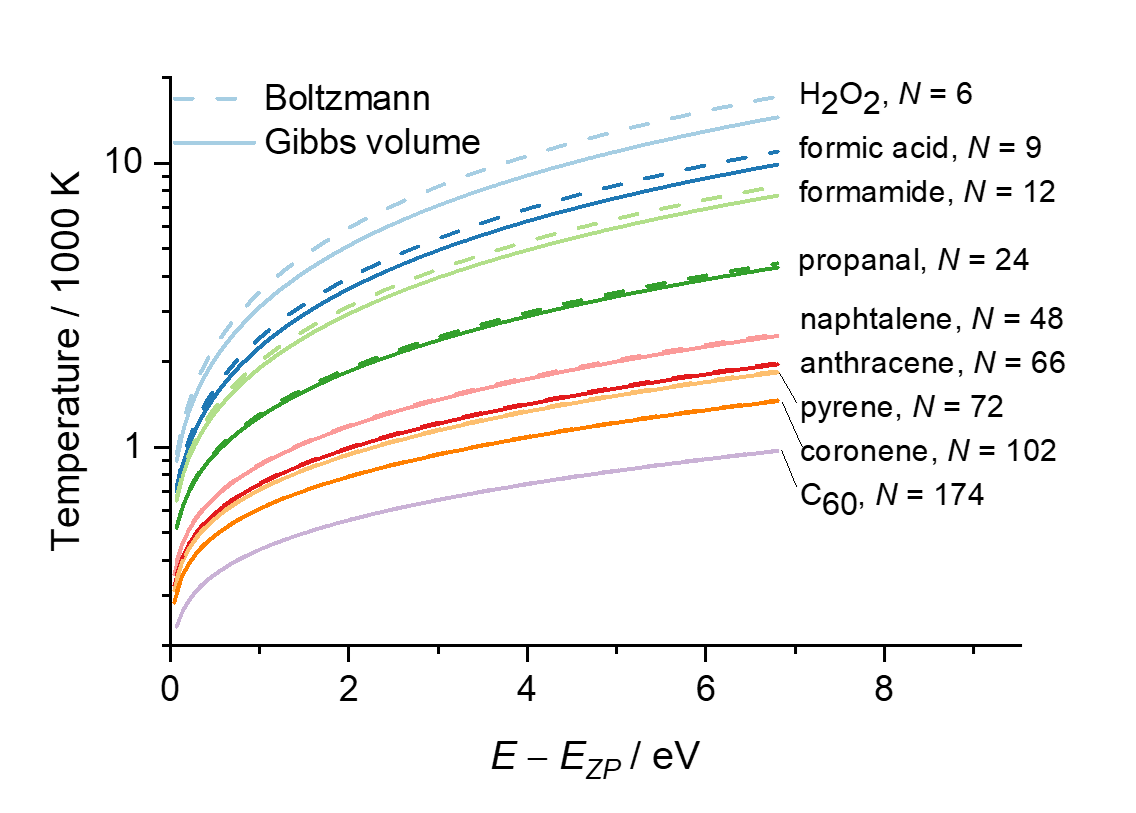
MB
Reference
[1] M. Barbatti, Defining the temperature of an isolated molecule, J. Chem. Phys. 156, 204394 (2022). DOI: 10.1063/5.0090205


0 Comments