Disentangling the Quantum Measurement Problem

What do we know (and don’t know) about quantum collapse?

At the World Science Festival held this spring, the renowned physicist Brian Greene engaged in a thought-provoking debate with three quantum mechanics specialists, asking about the quantum measurement problem or what happens to a quantum state when it is measured. It was unsettling to see all three proposing entirely distinct answers. Why, a century after the development of quantum mechanics, do we still lack a consensus on its most fundamental process? What do we truly understand about the quantum measurement problem?

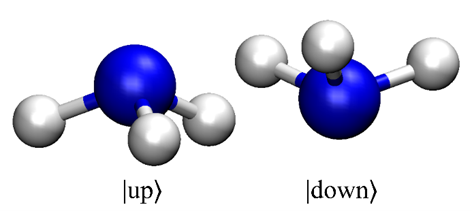
In quantum mechanics, all information about a physical system is encoded by the quantum state, a mathematical entity containing contributions from all possible outcomes of a measurement. Consider the ammonia molecule NH₃, for example. Its more stable geometry looks like a pyramid, with the three hydrogen atoms forming a triangular base and the nitrogen atom lying either above or below the base. Thus, putting aside molecular vibrations and rotations, the nuclear quantum state of this molecule has two terms corresponding to up and down pyramids. Let us be fancy and name them |up⟩ and |down⟩ states, respectively. The weight or amplitude of each state smoothly changes with time, obeying the Schrödinger equation, the master equation of quantum mechanics.

When we measure the system, we always observe one (and only one) outcome, with a probability that is the square of the corresponding state amplitude at the measurement time. In one instant, we may have a 25% probability of finding |up⟩ and a 75% probability of finding |down⟩. When we single out the outcome value, we say the quantum state collapsed.

This description of the quantum measurement raises three questions. First, what is the outcome basis we must use to write out the quantum state? In my example, I arbitrarily chose to describe it in terms of |up⟩ and |down⟩. However, I could have equally done it in terms of an outcome basis that mixes them (one possibility would be |+⟩ = |up⟩ + |down⟩ and |-⟩ = |up⟩ – |down⟩), and the quantum state would still be the same. Why do we observe certain types of outcomes but not others?

Second, let us take two solutions of the Schrödinger equation, multiply each of them by a constant, and sum these terms. The result, called a superposition, is also a solution. Therefore, nothing prevents the molecule from being in the |+⟩ state, a superposition of |up⟩ and |down⟩ (a molecular dead-alive Schrödinger’s cat). That is not an abstraction. Superpositions exist and have physical effects, such as interference patterns in the classic double-slit experiments. However, we do not usually observe them, especially in large systems, unless we employ exquisite experimental techniques. Why do we not see evidence of superposition everywhere?

Third, how and why does a quantum measurement select a specific outcome? Can the Schrödinger equation and the collapse be unified in a single theoretical framework?

Together, these three questions compose what we call the measurement problem.

Standard quantum mechanics, as taught at physics colleges, postulates that collapse must occur whenever a measurement is done. However, it does not explain which outcome basis should be used, why a collapse happens, or even what constitutes a measurement. The remarkable predictive power of quantum mechanics has led most physicists to adopt a pragmatic “shut up and calculate” approach. Yet, this knowledge gap in standard quantum mechanics has sparked a century of debates and a continuous quest for a more satisfactory description.

The World Science Festival debates made clear that, as of 2024, we are still far from a consensual explanation of the measurement problem. The first of Greene’s guests was the philosopher of physics, Elise Crull. She invoked decoherence to solve it. In the second debate, the physicist Sean Caroll claimed that the measurement problem is solved by the many-worlds hypothesis. He also dismissively admitted the existence of alternatives like objective collapse theories. The last debate was with the physicist Carlo Rovelli, who champions the relational interpretation, where the quantum state status, collapsed or superposed, is relative to the observer. Likely, had a fourth thinker been invited, they would have brought up another hypothesis. Wikipedia now lists thirteen distinct classes of theories and interpretations.

Decoherence, many worlds, objective collapse, relational interpretation. The cacophony of proposed solutions for the measurement problem is disturbing. It hurts our conception of science as delivering a consistent description of reality. Nevertheless, the situation is not as bleak as it seems.

The first two questions I listed are addressed by decoherence, the concept Crull invoked. Decoherence disperses the quantum information about a system into the surrounding environment, suppressing the observable effects of superposition. For example, information about |up⟩ and |down⟩ superposition in ammonia gas disappears almost instantaneously, within 10^‑19 seconds. Although the superposition persists in the ensemble of system plus environment, its effects become unobservable due to widespread dispersal in the gas.

Decoherence also leads to the environmental selection of a stable outcome basis through a process known as einselection. For a molecule in a gas, the environment-selected outcome basis for measuring nuclei is approximately position states (like |up⟩ and |down⟩), whereas for measuring electrons, energy states emerge as the preferred outcome basis.

Decoherence is part of standard quantum mechanics (although einselection is still a topic for research). It is an experimentally well-documented effect, crucial for quantum mechanical applications, such as quantum computing. Regardless of one’s preferred interpretation, the role of decoherence must always be considered.

We can also draw some insightful implications from decoherence. Before referring to it, we chose the {|up⟩,|down⟩} basis for describing the quantum state because it matches our classical intuition of nuclei as particles with defined positions. After decoherence, we realize that we likely developed such an intuition because the environment selects the {|up⟩,|down⟩} basis and suppresses superposition effects, creating the classical world of particles with well-defined positions.

Decoherence clears up a significant portion of the measurement problem. Nevertheless, it does not solve the third question. After the superposition is suppressed and the basis is chosen, the system rests on a mixture of possible outcomes. Decoherence does not provide any information on how and why only one of these outcomes is measured.

For some interpretations, this is not a problem. The many-worlds interpretation Caroll promoted, for instance, proposes that the remaining outcomes after decoherence correspond to independent universe branches. Observers in each of these branches perceive different outcomes because their quantum state, entangled with the molecular quantum state, is also branched. In one branch, the combined quantum state of the molecule and observer may be |up⟩|observer-sees-up⟩ and in another, |down⟩|observer-sees-down⟩. There are no branches with superpositions of both because decoherence suppressed them. Thus, the many-worlds interpretation implies the existence of one quantum universe composed of classical branches.

The many-worlds interpretation acquired somewhat shabby fame due to lazy sci-fi TV shows. Moreover, many people also feel threatened by the exuberant idea that we exist in parallel realities. (As for myself, I am captivated by the possibility that each of us is an infinitely branched holistic quantum being.) Despite the resistance, the many-worlds interpretation is a serious contender among the proposed solutions to the measurement problem. It is entirely consistent with standard quantum mechanics, and it does not require any modification of the theory. However, it must always be considered an interpretation (as opposed to a theory) as long as we cannot find a way to test it.

For the many-worlds interpretation, the quantum state has physical reality. Other interpretations take the opposite path. They claim that the quantum state is no more than a mathematical tool to predict outcomes. This is the stance of Rovelli’s relational interpretation and other interpretations as quantum Bayesianism, QBism for short.

Relational interpretation focuses on the interaction between systems. Properties, it claims, are only defined by the relation between the systems. Thus, the molecular geometry may be well-defined for an environment molecule nearby (acting as an observer) but still in superposition for another environment molecule that is too far away to act as an observer.

QBism takes a hard turn toward subjectivism. It considers that the quantum state only reflects the amount of our knowledge about the system. When we make a measurement and learn that the molecule is, say, |up⟩, its quantum state is immediately updated to tell that this term dominates, and the |down⟩ amplitude is null. Thus, what we call collapse is this process of updating the quantum state according to our knowledge level.

Just like in many worlds, we know no way to test relational interpretation and QBism. They must also be regarded as interpretations. Both are also entirely consistent with standard quantum mechanics.

The situation is profoundly distinct when dealing with the objective collapse theories. Those are, in fact, theories, not interpretations. They change the Schrödinger equation to account for the collapse.

In the most advanced objective collapse theories, the modified Schrödinger equation predicts that the system spontaneously, continuously, and randomly localizes in one of the outcomes, given enough time. No observers or interacting systems are required. The localization time depends on the mass of the system. For an isolated ammonia molecule in superposition, it may take billions of years for it to localize over |up⟩ or |down⟩. In a gas, however, localization happens instantaneously.

Objective collapse theories can be tested and eventually disproved. They posit, for example, that electrically charged particles in superposition should radiate during collapse. Experiments were recently conducted to measure such emissions, but their results were not conclusive.

The highest stakes among the objective collapse theories are with the Diósi-Penrose model. This theory claims that gravity is behind the term in the modified Schrödinger equation that induces collapse. This would happen because distinct mass distributions in the superposition (pyramide up or down in our example) would cause slightly different spacetime distortions, creating an instability that is resolved via collapse. The model predicts it takes billions of years to collapse an isolated molecule, but only 10^‑27 seconds to collapse a 10 kg body. (My research group has shown situations where the Diósi-Penrose collapse times could be unacceptably long for macroscopic systems.)

The Diósi-Penrose hypothesis has profound implications for physics. If it is proven, it means that gravity plays an exceptional role in nature. It would not only settle the measurement problem but also impact any future attempts at reconciling general relativity and quantum mechanics.

Here, I only touched on some of the leading proposed solutions to the measurement problem, which are still under serious consideration by physicists and philosophers. I left aside historically relevant but discredited hypotheses, such as the consciousness or the interaction between quantum and classical systems causing the collapse. I also did not discuss hidden-variable theories, which are still respectable contenders in the context of cosmic Bell experiments and superdeterminism. But that is a long story that I must leave for another occasion.

Gladly, today, the measurement problem is much less enigmatic than it was before decoherence was understood. Thanks to it, we know how the outcome basis is selected environmentally and why quantum interference is not easily observed. However, the measurement problem is still not entirely solved. We still cannot explain how and why we observe a single outcome.

Most scientists using quantum mechanics as a routine tool are pragmatically agnostic about interpretation. Others have chosen to be dedicated caretakers of their pet interpretation. I align with a third group, which believes we must continue the efforts to challenge the many hypotheses under the several interpretations and theories until, one day, the measurement problem in its totality will only be a topic for the history of science.

---

This essay was originally published at
Barbatti, M. (2024, June 21). The many answers to the quantum measurement problem.IAI News. /articles/the-many-answers-to-the-quantum-measurement-problem-auid-2871