Things have no well-defined position; light doesn’t illuminate. Seen from the Angstrom scale—the size of an atom, the universe is a pretty weird place.
In a previous post, I did a quick exercise relating the femtosecond, the time scale in which atomic phenomena take place, to diverse other aspects of life, the universe, and everything.
But since Einstein taught us that we can’t speak of d’Artagnan without speaking of the other three musketeers, that exercise wouldn’t be complete if I didn’t extend it for the spatial scale of the atoms, too.
Then, let’s talk about Angstrom.
One Angstrom (abbreviated Å) is defined as 10-10 m. In the same way as the femtosecond, the Å is one of those scales that are convenient for working but leave nothing for intuition. Down to those sizes, the world is pretty much different from our touch-and-see surroundings.
1. We can think of the atoms as soft spheres of 0.5 to 2 Å, depending on the type. But they are not the kind of things we could see even if we had a very, very powerful microscope. To see an object, it must be bigger than the wavelength of the light illuminating it. A wavelength of 1 Å, corresponding to 12.4 keV, is already in the X-ray region. Therefore, unless you’re a child from Krypton, atoms are just invisible under our normal red-till-violet light.
This doesn’t mean we can’t see atoms in indirect ways, as in these cool photos below, showing molecular reactions. The images were captured by Felix Fischer and his team in Berkeley, using a non-contact atomic force microscope. But with this technique, rather than photons, the microscope measures the electrostatic interaction between atoms in the sample and at those in the probe tip.
2. Let’s put the Å on a scale we can think about. First, if 1 Å were equivalent to 1 mm, then 1 mm would be equivalent to 10 km. That’s to say that if a crazy B-movie-type scientist invented some stretching rays, he would have to make sand grains as large as a city to get atoms up to 1 mm wide.
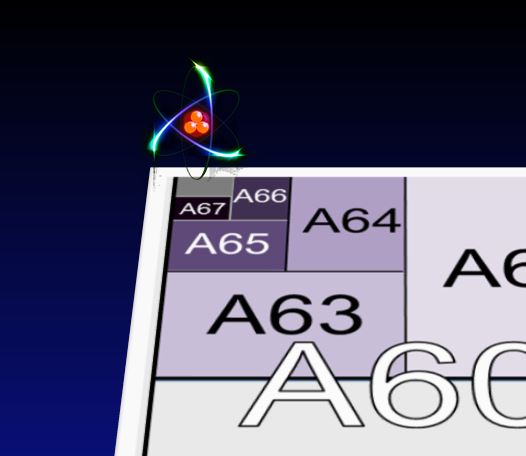
Now, consider this other thought experiment (it’s a bit less far-fetched but no less impossible): if you take an A0 page and cut the long side in two, you get an A1 page (just like in the left figure below). Repeat the process again and again, and you get the series of A2, A3, A4, … sizes. Do it 67 times and you will get an A67 page size with 0.7 Å x 0.5 Å, the dimensions of a single atom.
3. While the Å scale is small from our perspective, it’s far from being among the smallest sizes in the universe. The atomic nucleus is only 0.0001 Å. An electron is still 100 times smaller than the nucleus. (These two numbers imply that an atom is basically empty space. I still remember how this trivia fascinated me when I was a child.)
More impressive is the comparison of the Å scale to the Planck length (lP = 1.62 x 10-25 Å), the smallest measurable size in our universe, before spacetime collapses into a quantum soup. If 1 lP were 1 Å, then 1 Å would be 0.07 light-years, far larger than the solar system.
But things could be even smaller in the past. According to the inflationary model for the universe expansion, when the observable universe was 10-43 s old, its size was about 10-40 Å. It grew fast, though. The observable universe got to the Planck length by 10-35 s, and it was already 1 Å before completing its first 10-34 s. Now, that it’s 13.8 billion years old, the observable universe has a radius of 4.3 x 1036 Å (46 billion light-years).
4. Have you ever flown in one of those giant Airbus A380? I did it a few times. They are quite impressive machines with their 72.73 m length. Well, almost 72.73 m… Flying at 800 km/h, it should contract along the direction of motion due to relativistic effects. Someone standing on the ground and measuring the airplane length while it flies by would note that it’s 0.2 Å shorter than when it’s parked.
5. Of course, to measure anything with precision larger than 0.2 Å isn’t trivial. Indeed, it has even some weird implications due to the uncertainty principle of quantum mechanics.
Suppose, for instance, that we could know the position of a hydrogen atom with precision larger than 0.2 Å. Then, our uncertainty on the atom’s speed would necessarily be larger than 1500 m/s (not due to instrumental errors, but due to the laws of physics). This means that after 10 fs, the atom could have moved anywhere within a sphere of 0.2 Å radius, and we wouldn’t know it; just making useless the initial hyper-precise measurement of the position.
6. Finally, a recipe to destroy the world: our crazy scientist gave up his stretching rays and decided to build a gigantic compressor to squeeze the whole Earth’s atmosphere into a 90 Å box. He knows that if he succeeds, he will create a black hole, which will slowly suck all the planet into it. The plan couldn’t be eviler, could it?
MB
A bit of the mathematics to get the relations in this post:
A page A0 has area a0 = 1 m2. An A1 page has half of that, a1 = 1/2 m2. And so it goes through the whole series: an An page has area an = a0/2n. If we solve this last equation for finding which n (integer) gives a 1 Å2 area, we get n = 67. The height and width of the corresponding page are related to the A0 dimensions by hn = h0/2m and wn = w0/2m, where m = ceiling(n/2), for instance, ceiling(67/2) = ceiling(33.5) = 34.
The Planck length is defined as
lP = (ħGc-3)1/2 = 1.62 x 10-35 m,
where ħ is the reduced Planck constant, G is the gravitational constant, and c is the speed of light.
Length contraction in special relativity grants that a body with length L0 when it’s resting shrinks by δL when it moves with speed v. These quantities are related by
δL = (1-1/γ) L0 ,
where
γ = (1-v2/c2)-1/2.
The uncertainty principle states that
ΔxΔv ≥ ħ/2M,
where Δx is the position uncertainty and Δv is the speed uncertainty. I’m supposing we know the atom mass M with absolute precision.
The event horizon of a black hole with mass M is given by the Schwarzschild radius:
Rsh = 2GM/c2.
Earth’s atmosphere has a mass M = 5.1 x 1018 kg.
- This post is a revised version of a text first published in my former blog Much Bigger Outside on May 3, 2015.
- While you’re here, check my first fiction book, “One Billion Faces.“